Factor Analysis
Factor Analysis is a statistical technique used to identify underlying relationships among variables by reducing a large number of observed variables into a smaller number of latent factors. It aims to uncover the hidden dimensions or constructs that influence the observed variables, simplifying complex data structures and revealing patterns that are not immediately apparent.
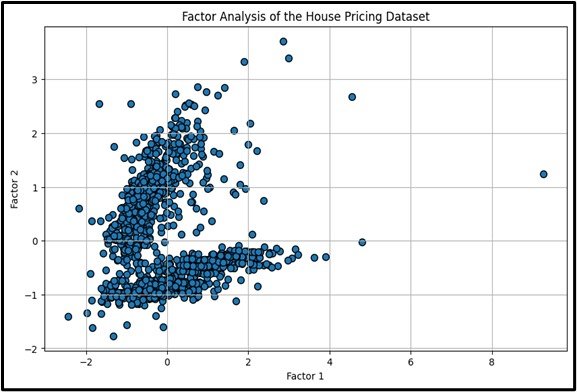
- Concept:Factor Analysis is a statistical method employed to uncover the underlying relationships between a set of observed variables.
- Latent Factors:The technique identifies latent factors or constructs that are not directly observed but influence the observed variables.
- Dimensionality Reduction:It reduces the complexity of the dataset by summarizing the information contained in multiple variables into a few factors, making data analysis more manageable.
- Applications:Factor Analysis is widely used in:
- Psychology: Identifying underlying constructs in psychological tests and surveys.
- Market Research: Understanding customer preferences and behaviors by reducing survey data into key factors.
- Social Sciences: Exploring underlying factors that influence various social phenomena.
Enhancing Model
Purpose: To reduce the dimensionality of the data and identify underlying latent factors that explain the observed correlations among variables.
Input Data: Numerical variables.
Output: A set of latent factors and their loadings on the observed variables.
Assumptions
Assumes that observed variables are influenced by a smaller number of unobserved variables (factors) that explain the correlations among them.
Use Case
Factor Analysis is useful in fields like psychology, finance, and social sciences to identify underlying constructs that explain the relationships among observed variables. For example, identifying underlying psychological traits from a set of behavioral data or determining economic indicators from various financial metrics.

Advantages
- Reduces the number of variables while retaining most.
- It helps to identify and understand the structure of the data.
- It is useful for data interpretation and constructing composite scores.

Disadvantages
- It is sensitive to the initial assumptions.
- Requires large sample sizes to produce reliable results.
- Interpretation of factors can be subjective and challenging.
Steps to Implement:
- Import required libraries such as `numpy`, `pandas`, and `sklearn`.
- Load and preprocess data: Load the dataset, handle missing values, and prepare features for Factor Analysis.
- Standardize the data: Optionally, use `StandardScaler` from `sklearn.preprocessing` to standardize the features, as Factor Analysis can be sensitive to the scale of the data.
- Import and instantiate FactorAnalysis: From `sklearn.decomposition`, import and create an instance of `FactorAnalysis`, specifying the number of factors.
- Fit the Factor Analysis model**: Use the `fit` method on the data to estimate the factors.
- Transform the data: Use the `transform` method to project the data onto the factors, reducing its dimensionality.
- Analyze the factor loadings: Examine the factor loadings to understand the relationship between the original variables and the extracted factors.
Ready to Explore?
Check Out My GitHub Code