Linear Regression
Linear Regression is a statistical method used to model the relationship between a dependent variable and one or more independent variables by fitting a linear equation to the data. The goal is to predict the dependent variable based on the values of the independent variables, with the relationship being represented by a straight line or a hyperplane.
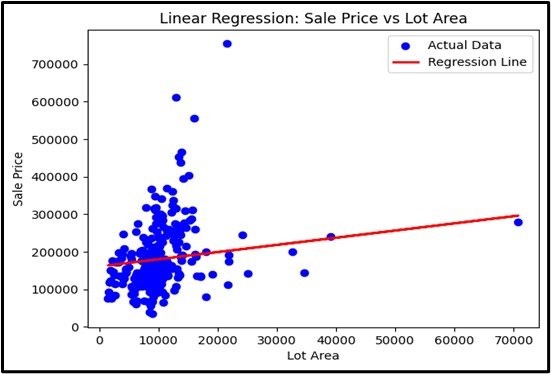
- Linear Relationship: Assumes a straight-line relationship between YYY and XXX.
- Simple Linear Regression: Involves one independent variable and is represented by Y=β0+β1X+ϵY = \beta_0 + \beta_1 X + \epsilonY=β0+β1X+ϵ, where β0\beta_0β0 is the intercept, β1\beta_1β1 is the slope, and ϵ\epsilonϵ is the error term.
- Multiple Linear Regression: Involves multiple independent variables and is represented by Y=β0+β1X1+β2X2+⋯+βpXp+ϵY = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p + \epsilonY=β0+β1X1+β2X2+⋯+βpXp+ϵ.
- Fitting the Model: Determines coefficients to minimize the sum of squared differences between observed and predicted values (least squares method).
- Applications: Used for prediction and understanding relationships in various fields, such as finance and biology.
Enhancing Model
Purpose: To predict the value of the dependent variable.
InputData: Basically it is a numerical variables.
Output: Continuous value.
Assumptions
Linearity, independence and the homoscedasticity, normal distribution of errors, and no multicollinearity.
Use Case
You can use Linear Regression when the connection between to the dependent and independent variables is mostly straight. For example, predicting how diabetes will get worse in patients based on features like age, sex, BMI, blood pressure, and other blood tests.

Advantages
- It is very simple to understand and implement.
- It does not take much computer power.
- Interpretable results.

Disadvantages
- It is Sensitive to outliers.
- Assumes linearity and other conditions that may not hold.
- Does not capture complex relationships in data.
Steps to Implement:
- Firstly, Import the libraries i.e. `numpy`, `pandas`, and `sklearn`.
- Load and preprocess data: Load the dataset, handle missing values, and prepare features and target variables.
- Split the dataset into training and testing sets using `train_test_split`.
- From `sklearn.linear_model`, import and create an instance of `LinearRegression`.
- Train the model: Use the `fit` method on the training data.
- Make predictions: Use the `predict` method on the test data.
- Evaluate the model: Check model performance using evaluation metrics like R-squared, MSE or MAE.
Ready to Explore?
Check Out My GitHub Code

