Ridge Regression
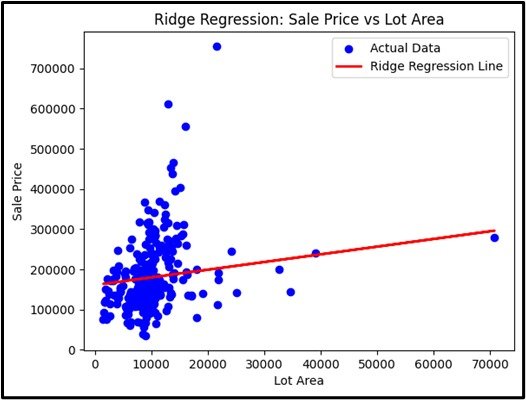
Ridge Regression is a type of linear regression that incorporates a regularization technique to prevent overfitting by adding a penalty term to the loss function. This penalty is proportional to the square of the magnitude of the coefficients. The purpose of the penalty is to shrink the coefficients of less important features, effectively reducing their impact on the model. By doing so, Ridge Regression helps in improving the model’s generalization to new data by balancing the fit and the complexity of the model.
Linear Relationship: Assumes a straight-line relationship between Y and X.
Simple Linear Regression: With one independent variable, it’s represented as Y=β0+β1X+ϵY = \\beta_0 + \\beta_1 X + \\epsilonY=β0+β1X+ϵ, where β0\\beta_0β0 is the intercept, β1\\beta_1β1 the slope, and ϵ\\epsilonϵ the error term.
Multiple Linear Regression: With multiple independent variables, it’s represented as Y=β0+β1X1+β2X2+⋯+βpXp+ϵY = \\beta_0 + \\beta_1 X_1 + \\beta_2 X_2 + \\dots + \\beta_p X_p + \\epsilonY=β0+β1X1+β2X2+⋯+βpXp+ϵ.
Fitting the Model: Ridge Regression fits the model by minimizing the sum of squared differences between observed and predicted values, with an added penalty term to shrink less important coefficients.
Applications: Commonly used in prediction and identifying relationships in fields like finance and biology.
Enhancing Model
Purpose: To improve the prediction accuracy and model stability.
Input Data: Numerical variables.
Output: Continuous value.
Assumptions
Same as linear regression but includes a penalty term for regularization.
Use Case
Use this algorithm when your data has features that are too closely related, or you want to avoid overfitting. For example, predicting house prices while considering many features and handling the problem of features being too closely related.

Advantages
- It reduces overfitting by adding regularization..
- It deals with features that are too closely related.
- Improves prediction accuracy for complex models.

Disadvantages
- Coefficients are biased.
- Requires tuning of the regularization parameter.
- May not handle non-linear relationships well.
Steps to Implement:
- First, Import the libraries i.e. `numpy`, `pandas`, and `sklearn`.
- Load and preprocess data: Load the dataset, handle missing values, and prepare features and target variables.
- Split the data: Use `train_test_split` to divide the data into training and testing sets.
- From `sklearn.linear_model`, import and create an instance of `Ridge`.
- Train the model: Use the `fit` method on the training data.
- Make predictions: Use the `predict` method on the test data.
- Evaluate the model: Check model performance using evaluation metrics like R-squared or MSE.
Ready to Explore?
Check Out My GitHub Code

